Level curves Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve C of value c and the trace on the plane z = c a level curve C always lies in the x y plane, and is the set C of points in the x y plane onWolframAlpha Widgets "Level Curve Grapher" Free Mathematics Widget Level Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a The level curves are parabolas of the form y2Zo ;
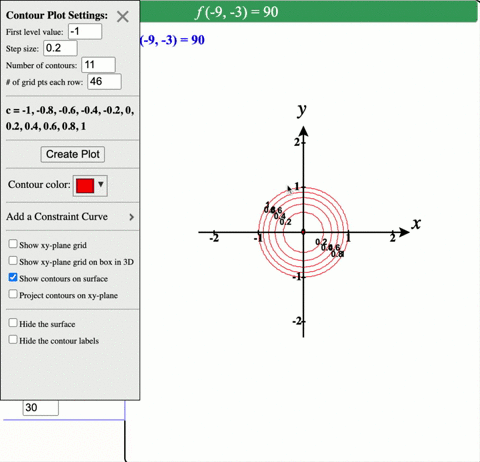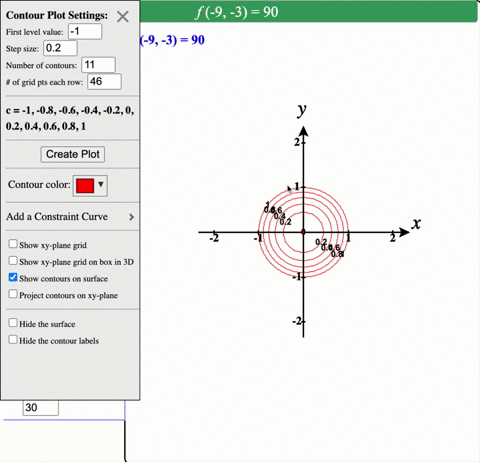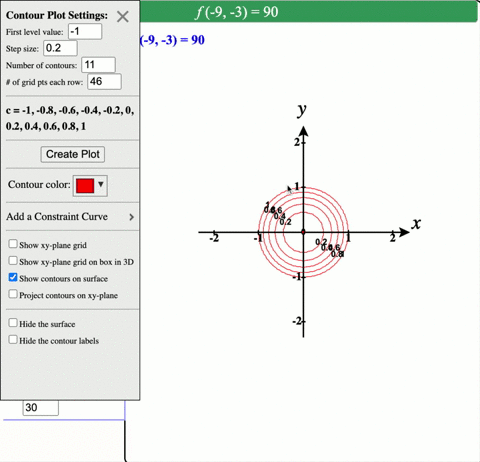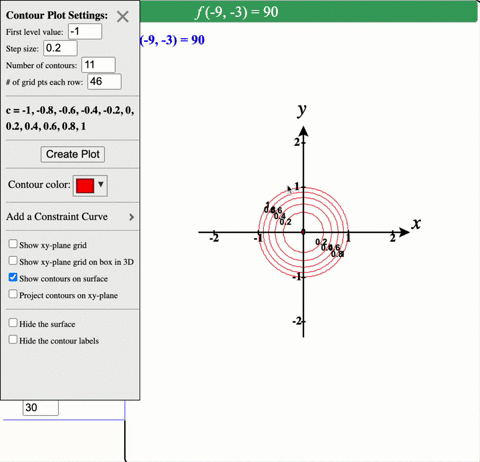
Solved Describe In Words The Level Curves Of The Paraboloid Z X 2 Y 2
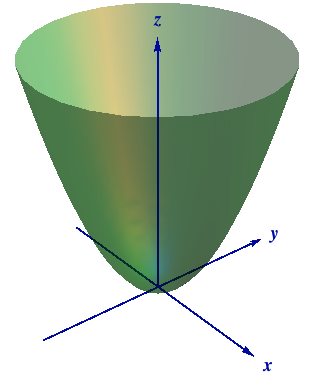
Elliptic paraboloid level curves
Elliptic paraboloid level curves-(b) Trickier still What would be the level curve/contour for the hyperbolic paraboloid at k= 0?Curves Circles The simplest nonlinear curve is unquestionably the circle A circle with center (a,b) and radius r has an equation as follows (x a) 2 (x b) 2 = r 2 If the center is the origin, the above equation is simplified to x 2 y 2 = r 2 The above equations are referred to as the implicit form of the circle The parametric form of



Level Curves
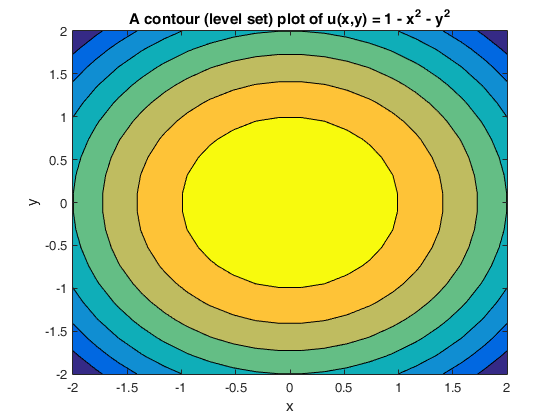
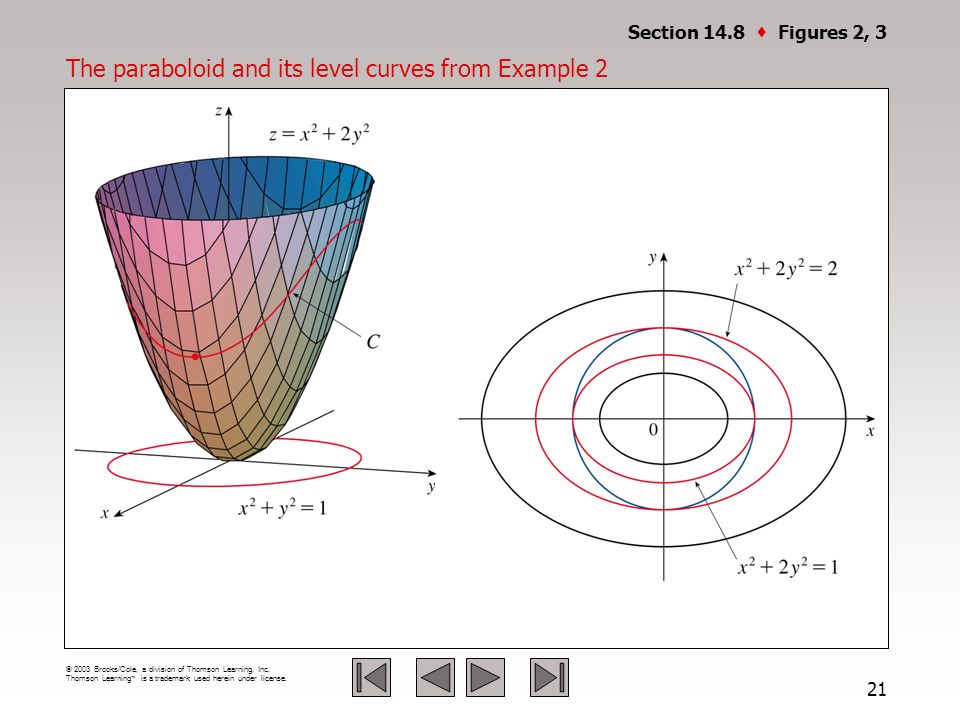
One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f ( x, y) is the curve of points ( x, y) where f ( x, y) is some constant value A level curve is simply a cross section of the graph of z = f ( x, y) taken at a constant value, say z = c Describe in words the level curves of the paraboloid z = x2 y2 Choose the correct answer below A The level curves are parabolas of the form x2 = zo B The level curves are lines of the form x y = C The level curves are parabolas of the form y2 = zo D The level curves are circles of the form x2 y2 = 2oGraphs of functions and level curves The elliptic parabolloid z = x2 y2 ParametricPlot3D@8Sqrt@tD Cos@uD, Sqrt@tD Sin@uD,t
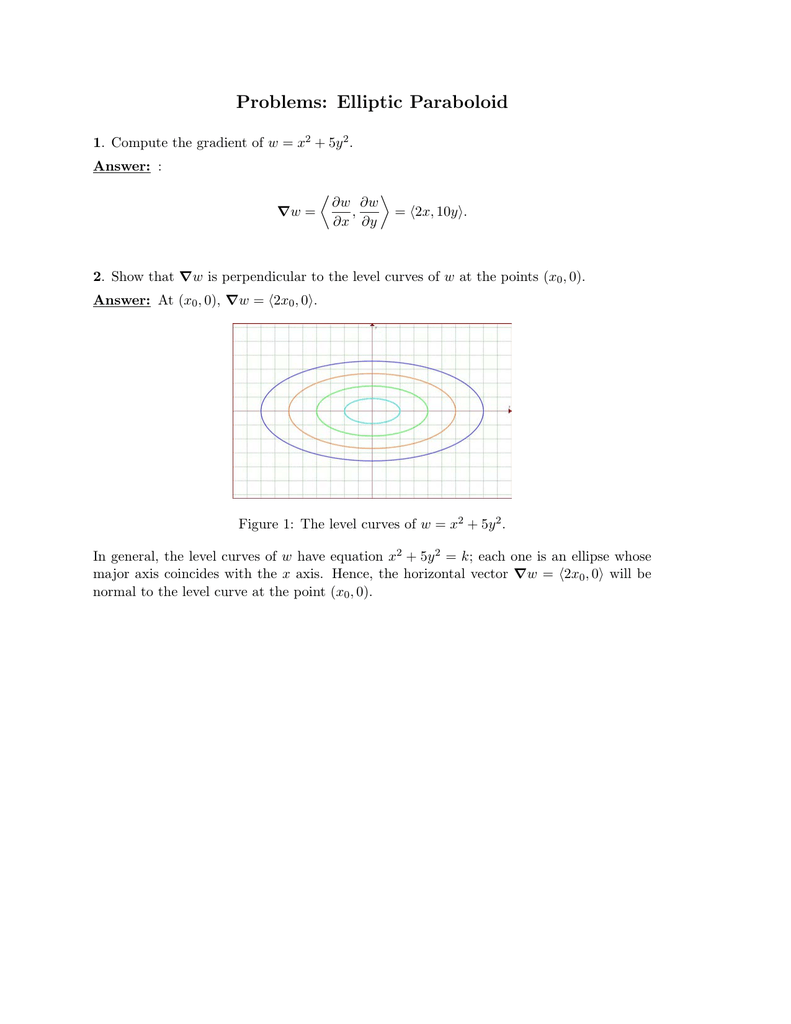
The animation below shows the paraboloid \(z=x^2y^2\) with \(\vec r(t) = \langle t, t, 2t^2\) tracing out its intersection with the plane \(y=x\) Further Questions Find a parameterization of the curve in the example that traces out the curve half as fastThere would be an in–nite number of intersecting lines (level curves/contours) (a) Consider the upper hemisphere z= p 1 x2 y2 What would be the level curve/contour for z= k= 1?Each one is an ellipse whose major axis coincides with the x axis Hence, the horizontal vector Vw = (2x 0, 0) will be normal to the level curve at the point (x 0, 0)
Level curves and surfaces The level curves of are curves in the plane along which has a constant value We will sketch level curves corresponding to a couples values, such as The level set is given by , or This is a parabola in as a function of Now we add the and level sets Solving for level curves of an elliptic paraboloid given by quadric surface equation Follow 18 views (last 30 days) Show older comments supernoob on 16 Jul (level curve) at a given height z, and to get the vertices of this ellipse It would be nice to plot the ellipse, too I have to do this over and over again, so the fastest way wouldSo consider for a paraboloid graph, whose level curves are circles, the gradient points radially outward from the origin The relationship between the two is shown in the next graph As the gradient, whose form for a paraboloid with a circular crosssection is 〈 〉, get closer to the origin they get shorter, and further



1




Problems With Level Curves New To Julia Julialang
Level Curves of a Paraboloid This example requires WebGL Visit getwebglorg for more info When we lift the level curves up onto the graph, we get "horizontal traces"Question 1327 Describe in words the level curves of the paraboloid z=x y2 Choose the correct answer below A The level curves are lines of the form x y=Zo O B The level curves are circles of the form x2 y2 ° C The level curves are parabolas of the form x2Zo 0 DAccording to the internet, finding the circumference of paraboloid level curves seemed a tad too easy It said to simply plug in the z value or the height level into the formula c = x^2 y^2 or something like that, square root the c value to get the level curve circles radius For example at z = 1 the circles radius would be square root 1 aka 1




Paraboloid Wikipedia




Paraboloid Wikipedia
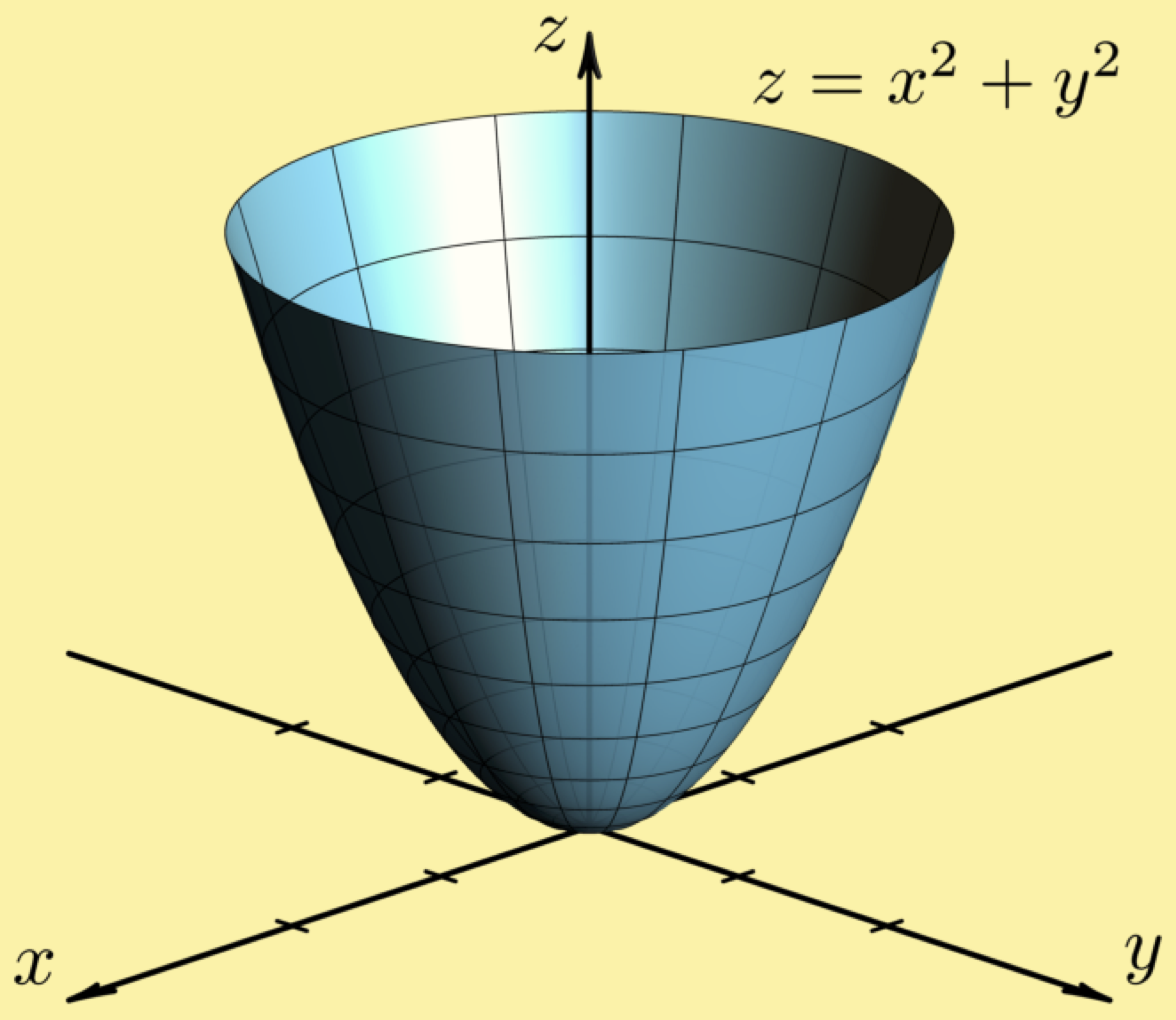
This is an elliptic paraboloid and is an example of a quadric surface We saw several of these in the previous section The next topic that we should look at is that of level curves or contour curves The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is anyFor this question They give us the privilege 16 minus X squared over four minus y squared over 16 And they wanted to show that a tangent lines the level care but see 16 minus X squared over four minus y squared over 16 is equal to quote So this is our love worker They want us to show at the given point The slope at this point is equal to the radium Describe the level curves of the function z = 2x2 y2 1 for c = 0,2,3 Answer Ellipses 2 Sketch several level curves for the paraboloid z = 4 x2 y2 3 Describe the level surfaces of the function F(x, y, z) = 9 x2 y2 – 22 Answer Level surfaces are spheres x2 y2 z2 = p2 (0



1



Contours 3 Html
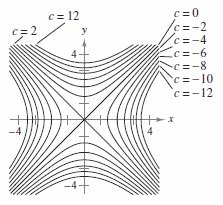
The entire enterprise of Lagrange multipliers (which are coming soon, really!) rests on it So here's another, equivalent, way of looking at the tangent requirement, which generalizes better Consider again the zooms in figure 4Solution If I slice the cone with cuts parallel to the xyplane at even intervals (for example, at z= 1, z= 2, z= 3, etc), then the radius of the circles grow linearlyExample 8 Describe the level curves of g(x,y) = y2 − x2 from Examples 4 and 5 Answer Figures A8a and A8b • The level curves g = c is a hyperbola with the equation y 2− x = c (The surface is a "hyperbolic paraboloid") Level curves of g(x,y) = y2 −x2 Figure A8a Figure A8b



Howtoplotfunctiontwovariables



Hyperbolic Paraboloid Geogebra Dynamic Worksheet
2The level curves for the cone (graph ~) and the paraboloid (graph }) are both concentric circles How did you determine which set of level curves match the cone?Scroll down to the bottom to view the interactive graph This graph illustrates the transition from a hyperboloid of one sheet to a hyperboloid of two sheets Consider the equation x 2 y 2 − z 2 = C In case if C > 0, the level curves x 2 y 2 = C k 2 are circles at any level z = k Therefore, the surface continues from negative z toPlotting Level Curves of an Elliptic Paraboloid Plotting Level Curves of an Elliptic Paraboloid
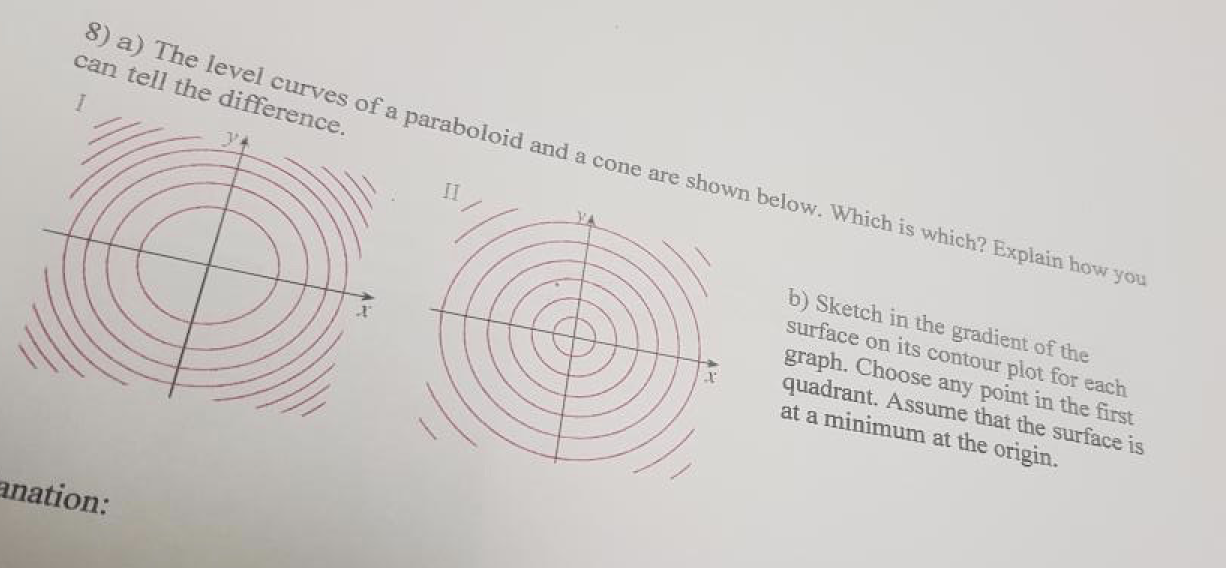



Solved 8 A The Level Curves Of A Paraboloid And A Cone Are Chegg Com



2
Level curves Level surfaces Worked problems Chapter 13 Vector Functions Chapter 14 Partial Derivatives cooling towers etc as is the hyperbolic paraboloid Again we can investigate what happens as these surfaces are sliced by planes parallel to the coordinate planesAnswer This requires a triple integral In a triple integral the integrand is the density function, so take this equal to 1 V=\int \int \int_{V} 1 dx dy dz Then transform the paraboloid, describing it in cylindrical coordinates In this example I'll use z=x^2y^2 between z=0 and z=1 In cylLevel Curves (ie Contours) and Level Surfaces Consider a function For any constant we can consider the collection of points satisfying the equation This collection of points is generally called a level surfaceWhen we generically have a (true 2dimensional) surface For example The level surface of at level is the unit sphere (the sphere of radius 1 centered at the origin)



Level Curves



Level Curves Part 2 Cone Hyperboloid Ellipsoid Youtube
A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value, on every point of the curve Different level curves produced for the f(x,y) for different values of c can be put together as a plot, which is called a level curve plot or a contour plotPlot the contour plot (level curves) of the same hyperbolic paraboloid > contourplot( f, x = 4 4, y = 4 4, scaling = constrained ) ;Z= x2 y2 = 0 8 If we have a 3var function, then we no longer




Math 0 Theory




Calculus Iii Functions Of Several Variables
Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign upThe advantage of level curves over graphs is that you already have a lot of practice drawing curves in \(\R^2\), but you probably don't have much practice drawing surfaces in \(\R^3\) Here are some computer generated images of paraboloids, one elliptic (level curves are ellipses) and one hyperbolic (level curves are hyperbolas)The level curves in this case are just going to be lines So, for instance, if we take the level curve at z equals 0, then we have just the equation 2x plus y equals 0 And so that has interceptso we're looking atso 0 equals 2x plus y, so that's just y equals minus 2x So that's this level curve That's the level curve at z equals 0




Paraboloid An Overview Sciencedirect Topics



Math Bu Edu
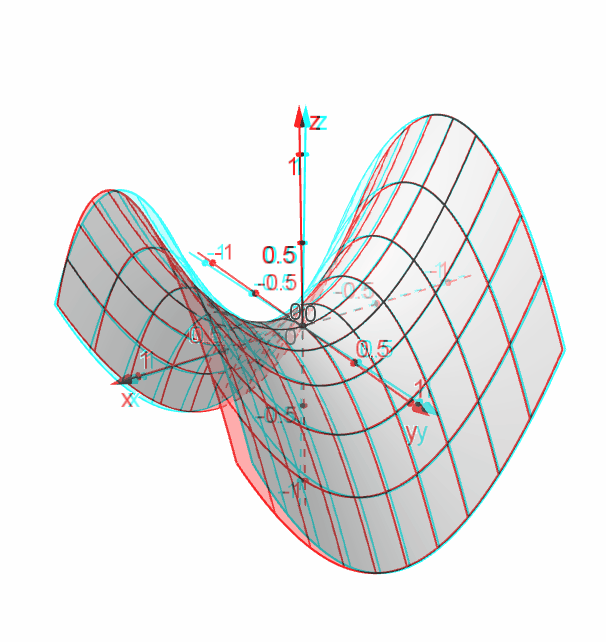
This surface is called a hyperbolic paraboloid because the traces parallel to the \(xz\) and \(yz\)planes are parabolas and the level curves (traces parallel to the \(xy\)plane) are hyperbolas The following figure shows the hyperbolic shape of a level curve To view the interactive graph Make sure you have the latest version of Java 7Two Model Examples Example 1A (Elliptic Paraboloid) Consider f R2!R given by f(x;y) = x2 y2 The level sets of fare curves in R2Level sets are f(x;y) 2R 2 x y2 = cg The graph of fis a surface in R3Graph is f(x;y;z) 2R3 z= x2 y2g Notice that (0;0;0) is a local minimum of f The level functions for paraboloid and the level function for ellipsoid are given This is what I've done so far I found the equation of the curve that forms from the intersection c(x,y) = curve of paraboloid and ellipsoid intersection The tangent vector at p(x1,y1,z1) on curve should be the same as the tangent vector at same point on



Calculus Iii 13 01 Functions With Several Variables University




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
If one imagines lifting each level curve z units off the page (where z is the zcoordinate associated with that level curve), a sequence of crosssections of the paraboloid is obtained which helps in its visualisation It is a theorem that the gradient vector, which for each point of a surface indicates the direction in which the surface isFigure 16 shows both sets of level curves on a single graph We are interested in those points where two level curves are tangent—but there are many such points, in fact an infinite number, as we've only shown a few of the level curvesDescribe in words the level curves ofthe paraboloid z = x y Choose the correct answer below The level curves are lines of the form x y = zo The level curves are parabolas of the form x The level curves are circles of the form x y The level curves are parabolas of the form y Find the domain of the following function g(x,y) = In (x 7 — y)




Polar Coordinates In Tikz Addplot3 Tex Latex Stack Exchange




Level Curves
A hyperbolic paraboloid (not to be confused with a hyperboloid) is a doubly ruled surface shaped like a saddleIn a suitable coordinate system, a hyperbolic paraboloid can be represented by the equation = In this position, the hyperbolic paraboloid opens downward along the xaxis and upward along the yaxis (that is, the parabola in the plane x = 0 opens upward and the parabolaThe Gradient Vector – GeoGebra Materials The gradient at each point is a vector pointing in the ( x, y) plane You compute the gradient vector, by writing the vector ∇ F = ∂ F ∂ x 1, ∂ F ∂ x 2, , ∂ F ∂ x n You've done this sort of direct computation many times before SoQuestion Vega was a rambling, and they want us to look at the level curve Let's see over form minus y squared over 16 at the level curve When this probably it is equal to 12 They wanted to also look at a point Let's see point for common zero Ensure that the grading and is there thought going to the tangent line at that point, so grating
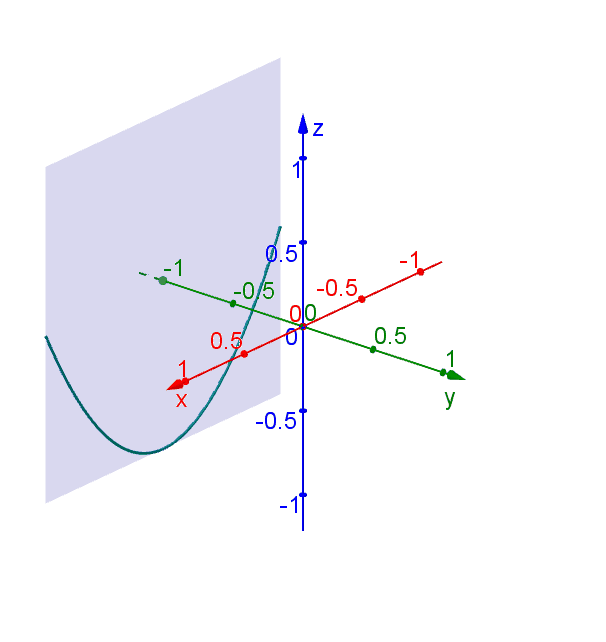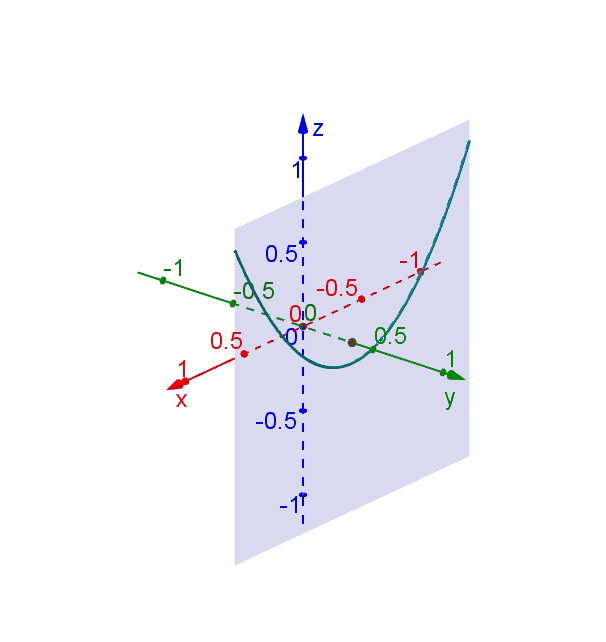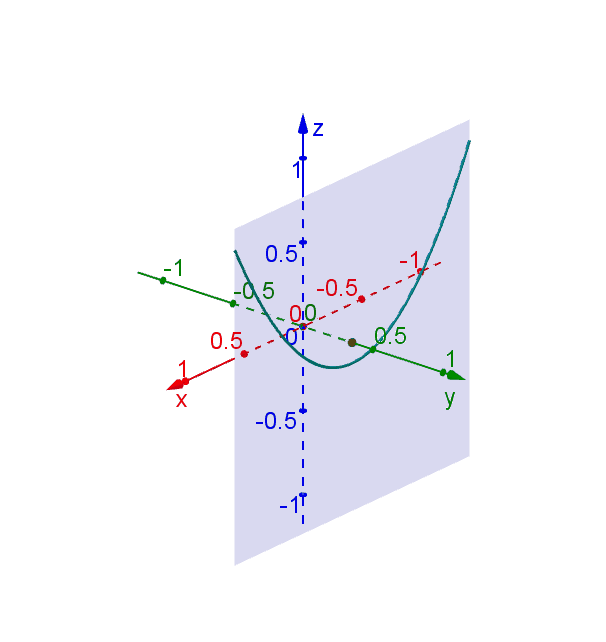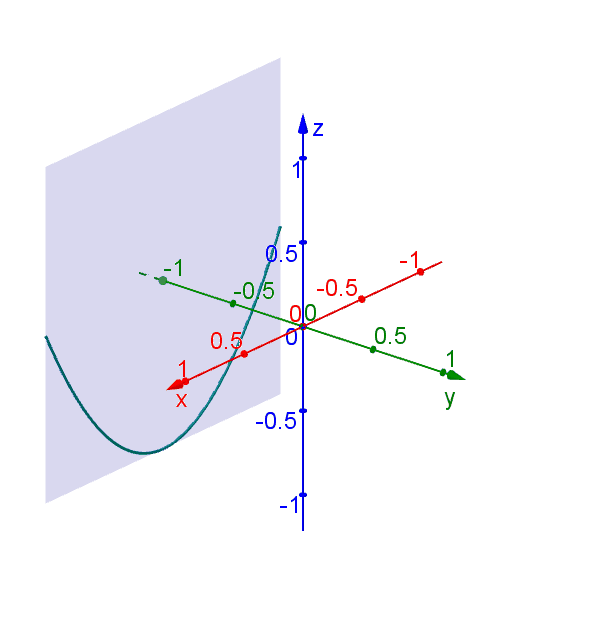



Hyperbolic Paraboloid Geogebra Dynamic Worksheet




Solved Level Curves Consider The Paraboloid F X Y 16 X 2 4 Y 2 16 And The Point P On The Given Level Curve Of F Compute The Slope Of The Line Tangent To The
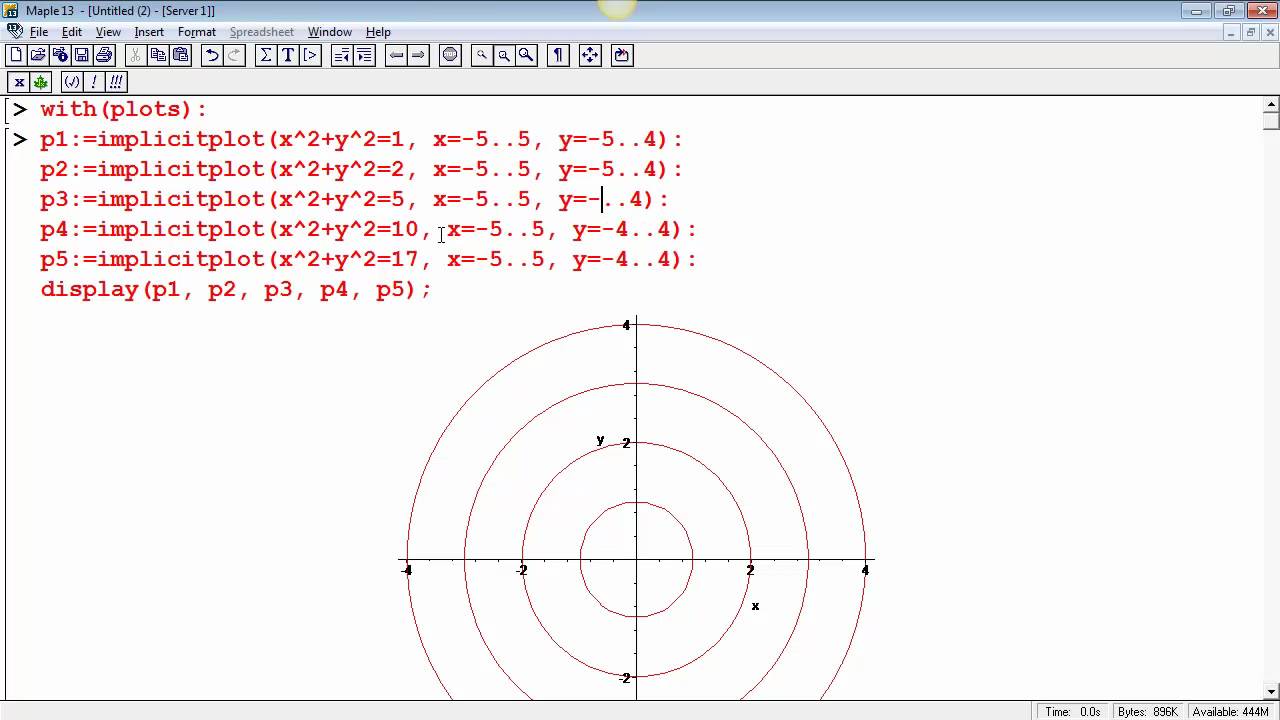
Would call these contours, but we call them level curves To nd a level curve, you just choose a height z = c and then write down the equation f(x;y) = c, where f(x;y) is the formula for the original function For example, for the function z = x 2 y2, level curves are the graphs of x y2 = c, for various values of c If c > 0, then these curvesThe curve $100=2x2y$ can be thought of as a level curve of the function $2x2y$;Figure 1 The level curves of w = x 2 5y 2 In general, the level curves of w have equation x 2 5y 2 = k;



Level Curves And Contour Plots Mathonline




Saddle Point Wikipedia
Figure 4 Level curves of the paraboloid, intersecting the constraint circle This intuition is very important;For example, the level curve of the paraboloid at Z=4 is the circle Therefore, the gradient of a function (which represents the rate of fastest change) is always perpendicular to its level curves because it is a vector that takes the direction of maximum increase in fSketch several traces or level curves of a function of two variables equation describes a circle with radius centered at the point Therefore the range of is The graph of is also a paraboloid, and this paraboloid points downward as shown



Elementary Calculus Example 4 Hyperbolic Paraboloid




Functions Of Several Variables
Figure 961 The graph of a curve in space Thus, we can think of the curve as a collection of terminal points of vectors emanating from the origin We therefore view a point traveling along this curve as a function of time \(t\text{,}\) and define a function \(\vr\) whose input is the variable \(t\) and whose output is the vector from the origin to the point on the curve at time \(t\text{}\)The surface defined by this function is an elliptical paraboloid This is a bowlshaped surface The bottom of the bowl lies at the origin The figure below shows the level curves, defined by f(x,y)=c, of the surface The level curves are the ellipses 4x^2y^2=cC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D
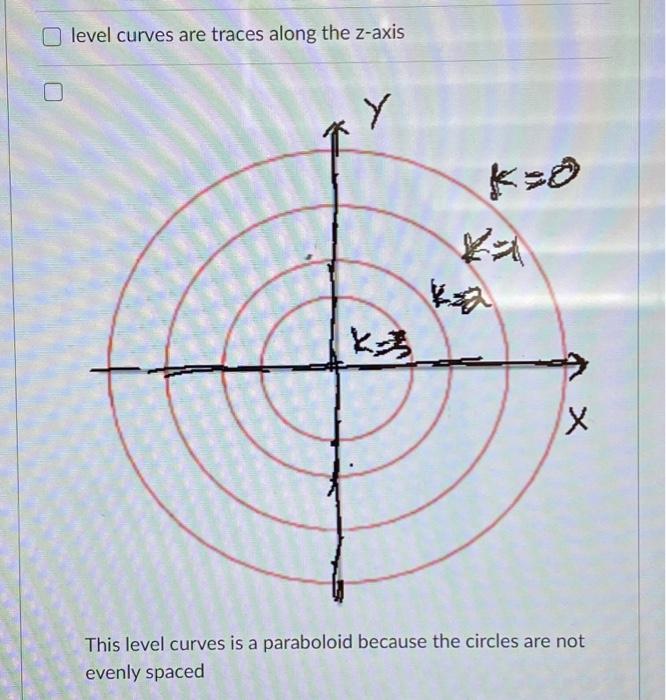



Solved Question 1 2 Pts Select All Statements That Are True Chegg Com



1
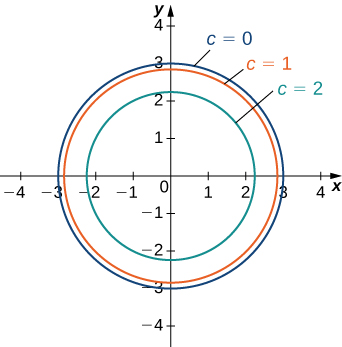



Level Curves Functions Of Several Variables By Openstax Page 3 12 Jobilize



Level Curves And Contour Plots Mathonline



0 3 Visualizing Functions Of Several Variables




Image Level Curves Of A Hyperbolic Paraboloid Math Insight
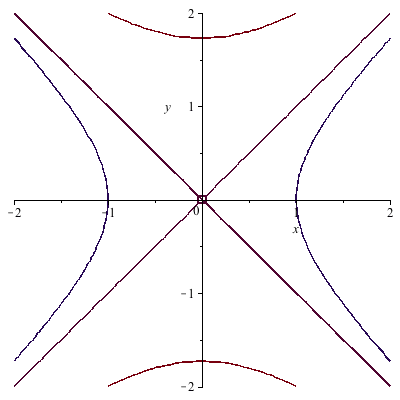



Partial Derivatives Gradients And Plotting Level Curves
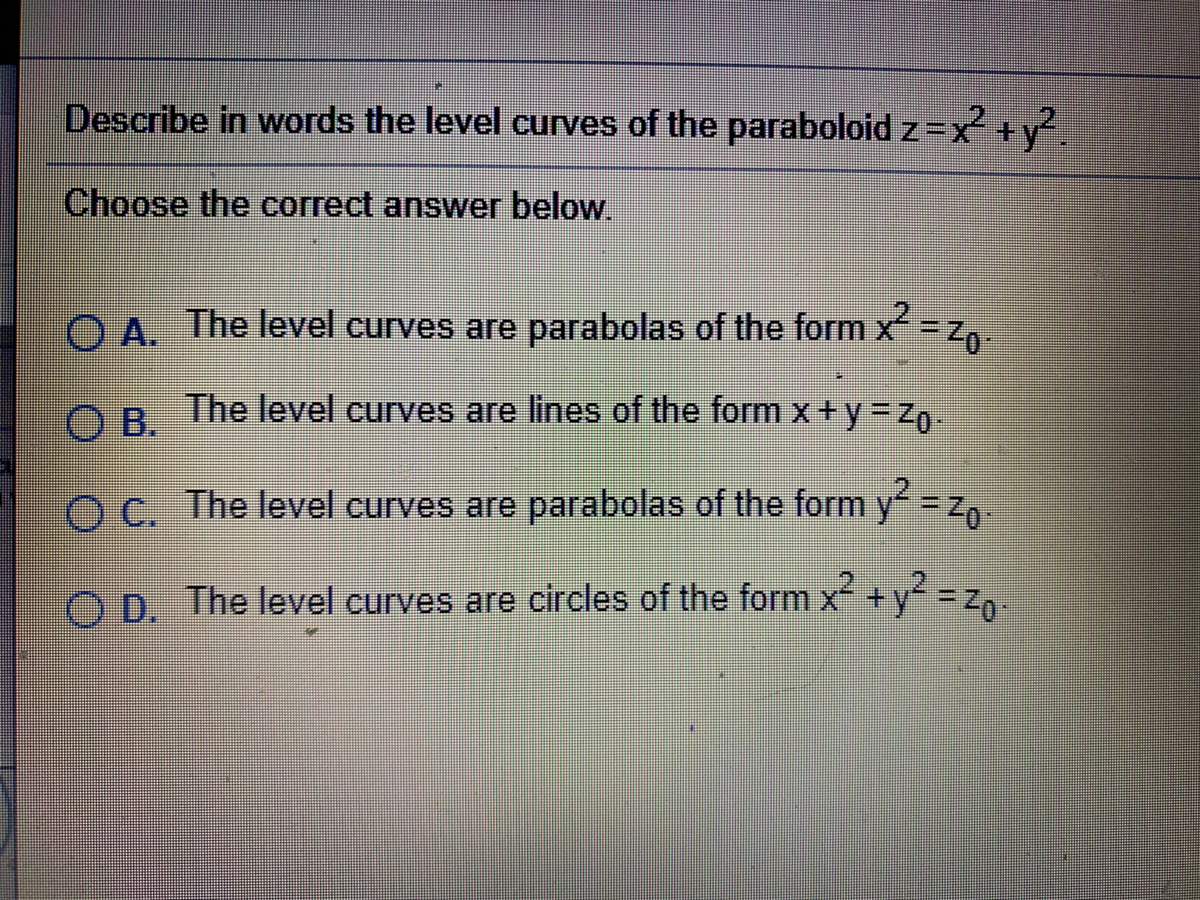



Answered Describe In Words The Level Curves Of Bartleby




Solved Describe In Words The Level Curves Of The Paraboloid Z X 2 Y 2




O7vwhmu1ihum
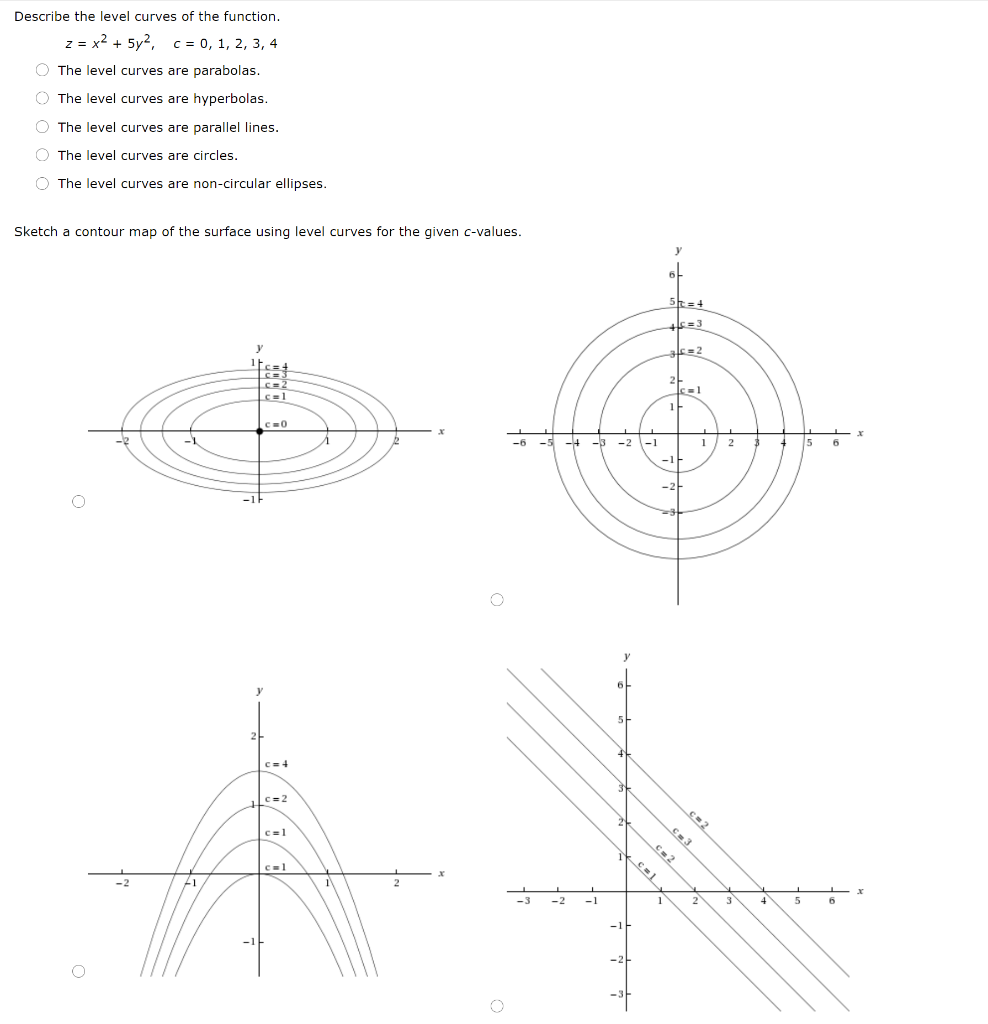



Solved Describe The Level Curves Of The Function Z X2 Chegg Com
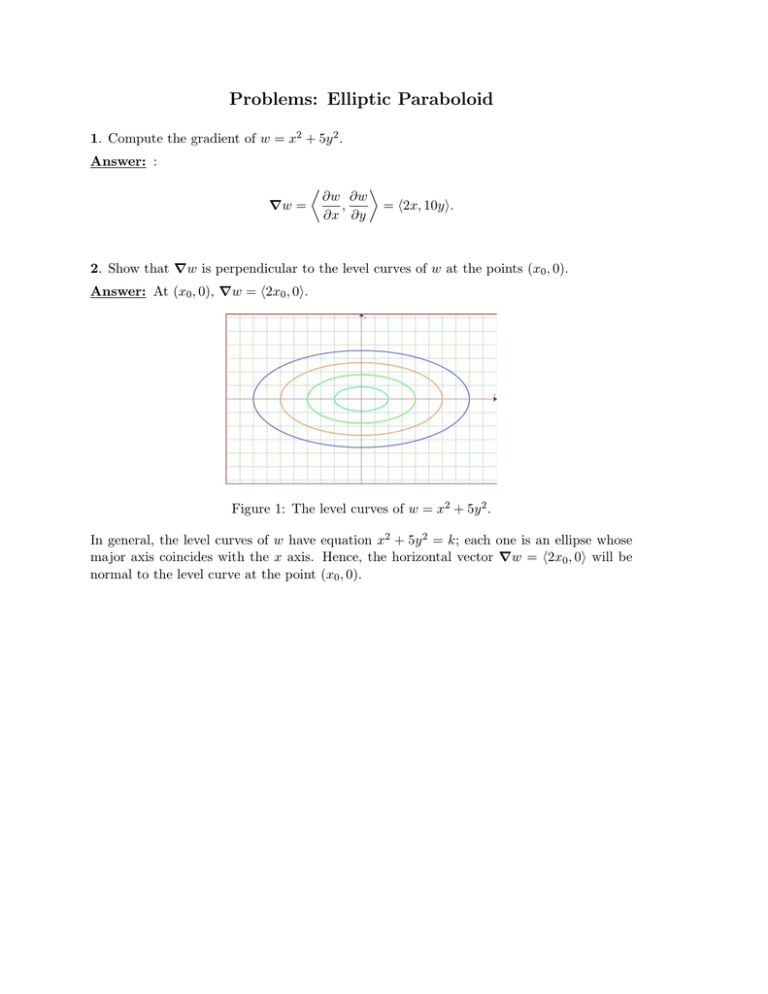



Problems Elliptic Paraboloid
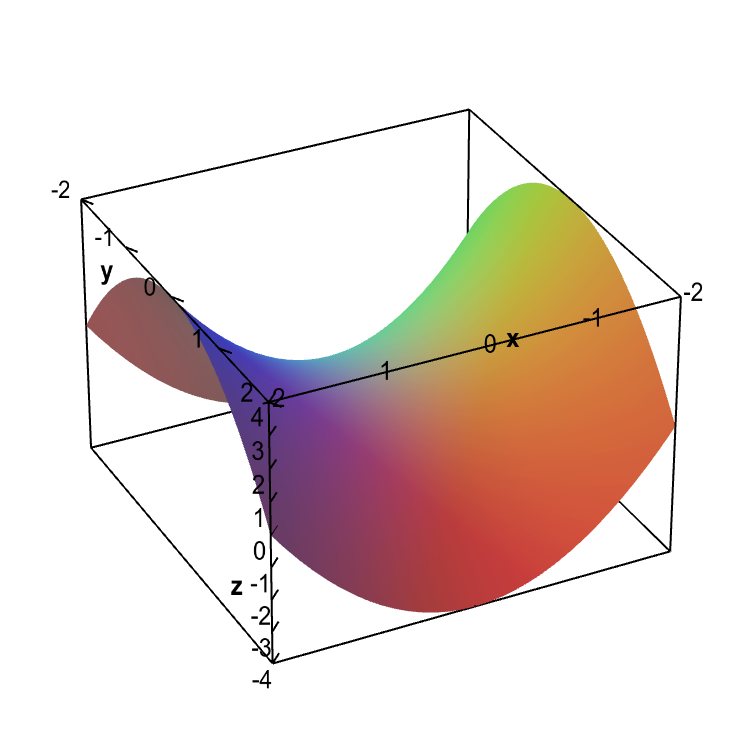



Level Set Examples Math Insight



The Gradient And Directional Derivative




Level Sets Ximera
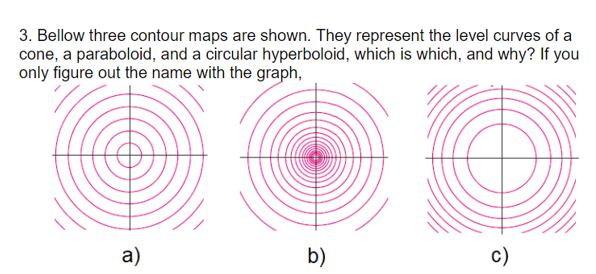



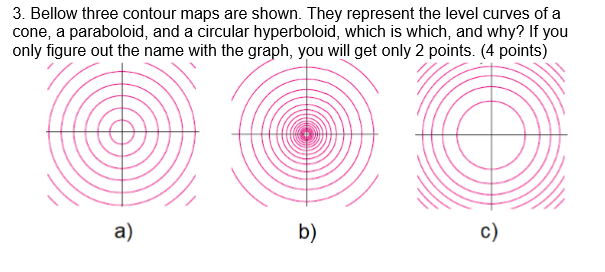
Solved 3 Bellow Three Contour Maps Are Shown They Chegg Com



Animated Demonstrations For Multivariable Calculus



Contour Plot Using Python And Matplotlib Pythontic Com
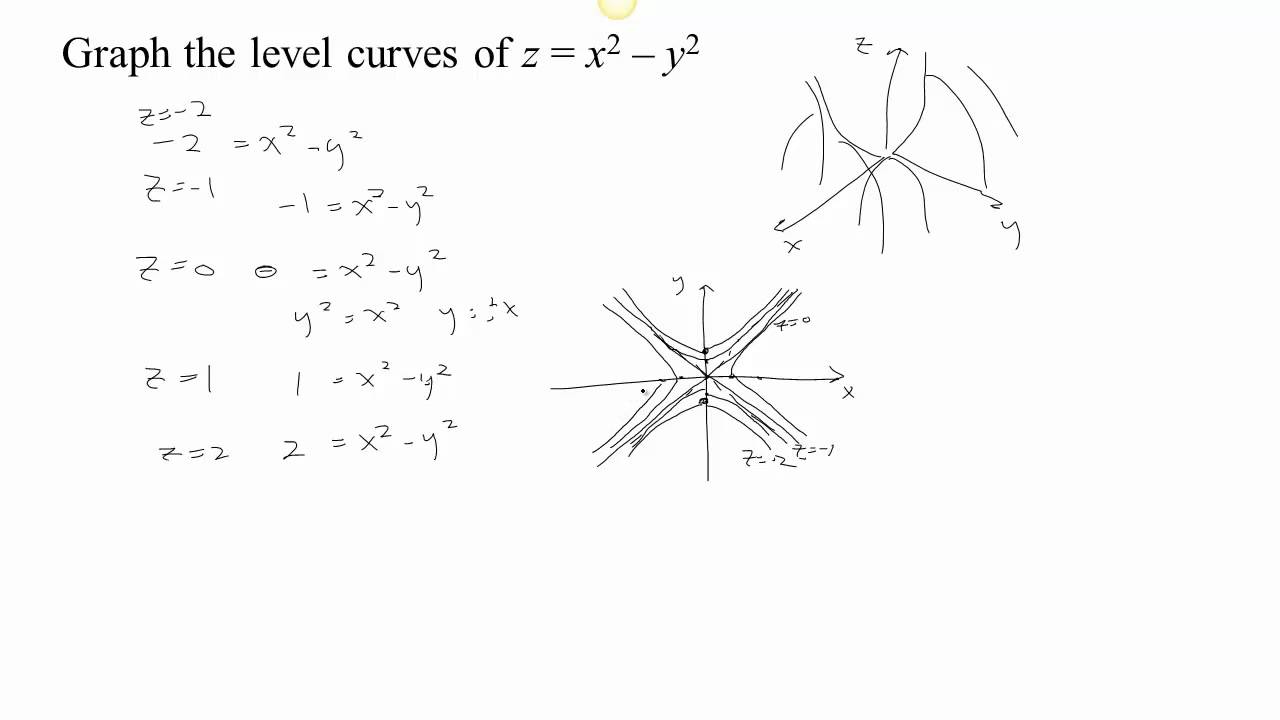



Level Curves Part 1b Hyperbolic Paraboloid Youtube
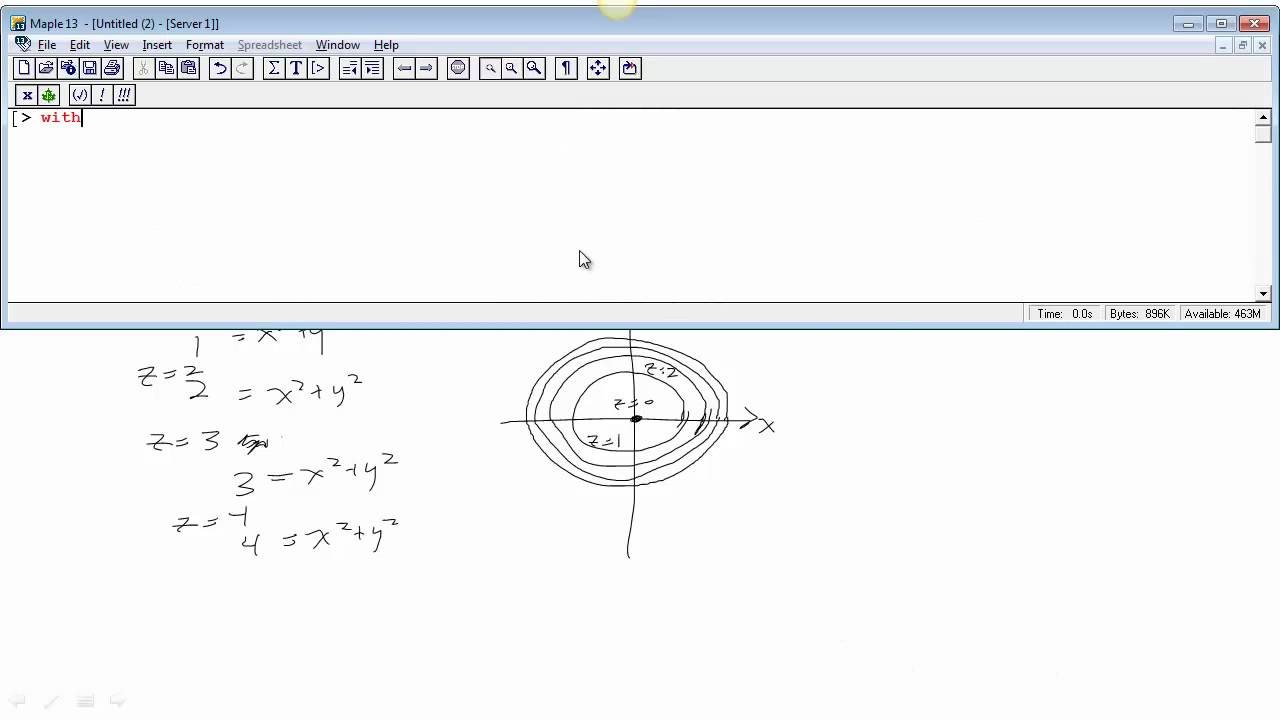



Level Curves Part 1 Elliptic Paraboloid Youtube




Level Surfaces



Hyperbolic Paraboloid With Level Curves M3dp Net




Applet Level Curves Of An Elliptic Paraboloid Shown With Graph Math Insight
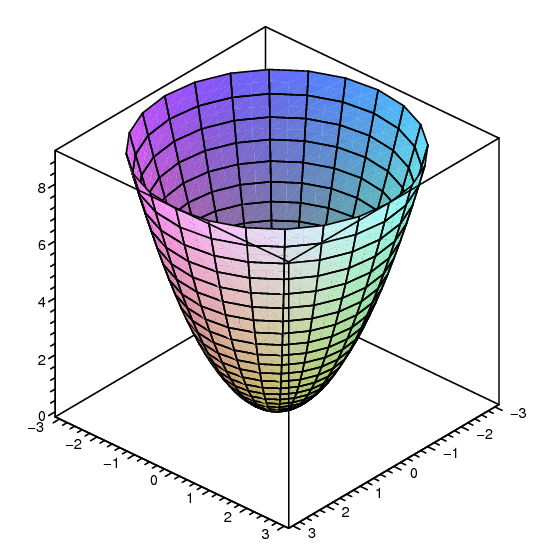



14 1 Functions Of Several Variables
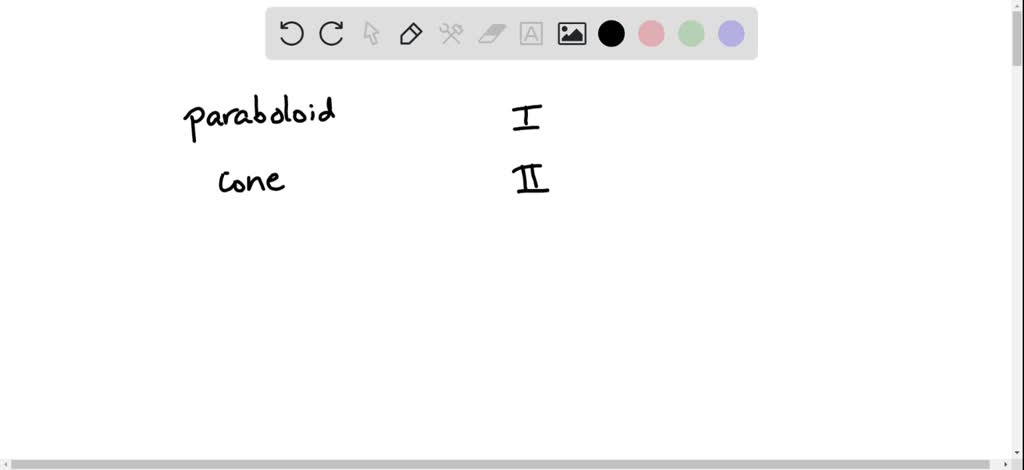



Solved Bellow Three Contour Maps Are Shown They Represent The Level Curves Of A Cone Paraboloid And Circular Hyperboloid Which Is Which And Why If You Only Figure Out The Name With The




Solved Level Curves Consider The Paraboloid F X Y 16 X 2 4 Y 2 16 And The Point P On The Given Level Curve Of F Compute The Slope Of The Line Tangent To The




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
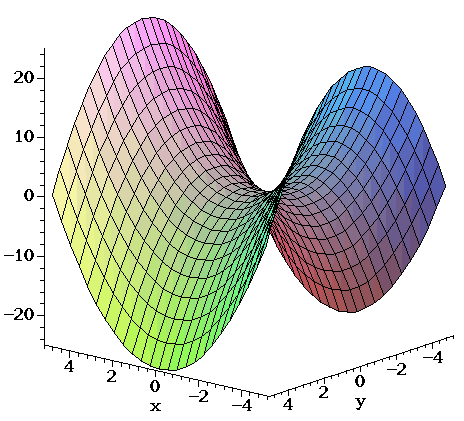



Surfaces Part 2




Image Elliptic Paraboloid Level Curves Math Insight




Applet Level Curves Of An Elliptic Paraboloid Shown With Graph Math Insight




Functions Of Several Variables




Calculus Iii Functions Of Several Variables
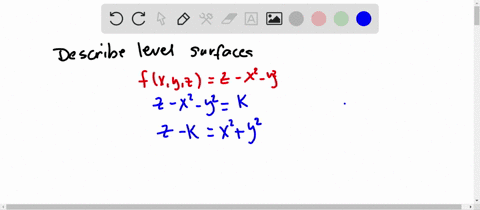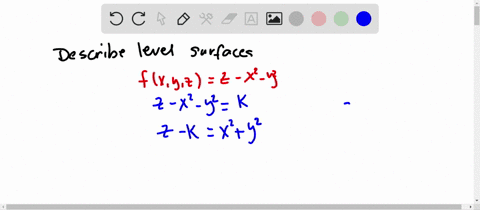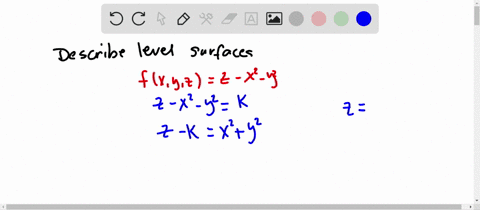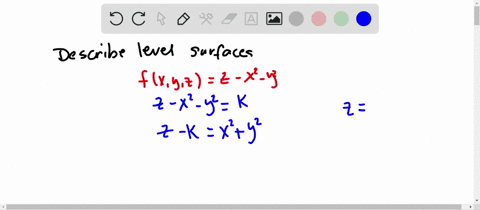



Solved Describe In Words The Level Curves Of The Paraboloid Z X 2 Y 2




Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



2
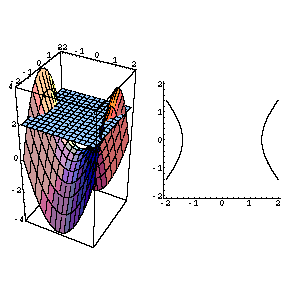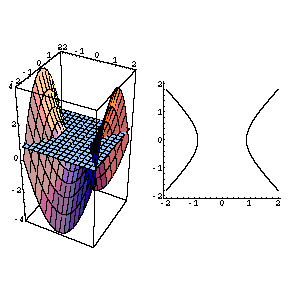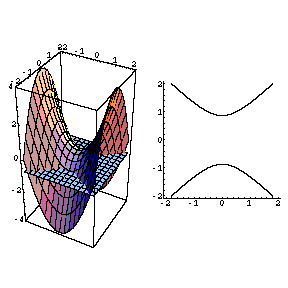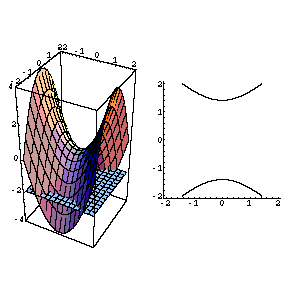



The Movie Hyperbolic Paraboloid




Calculus Iii Functions Of Several Variables
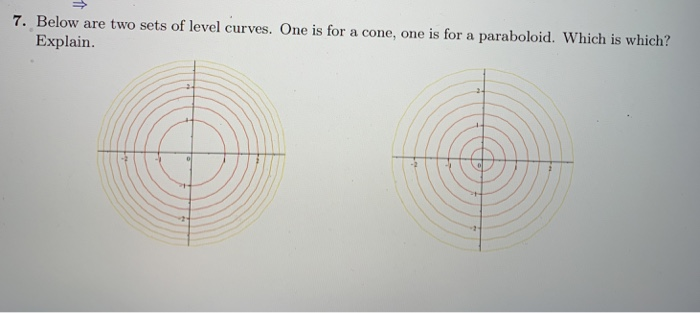



Solved 7 Below Are Two Sets Of Level Curves One Is For A Chegg Com



Surfaces And Traces




Applet Level Curves Of A Hyperbolic Paraboloid Math Insight




This Type Of Math Is Multivariable Calculus 1 7 Sketch The Level Curves Of F X Y P 16 X Homeworklib



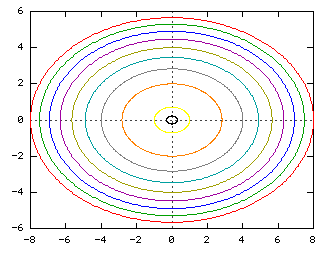
Level Sets Ximera




Cross Section Of The Caustic Of A Paraboloid Of Revolution In The Y 0 Download Scientific Diagram




Functions Of Several Variables
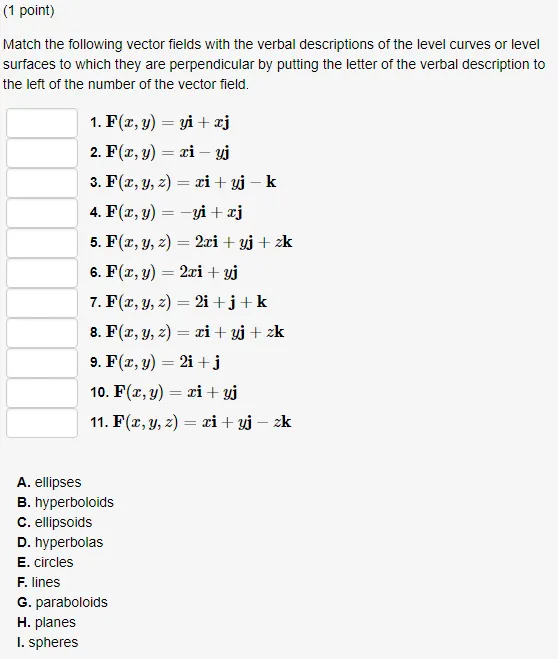



Oneclass 1 Point Match The Following Vector Fields With The Verbal Descriptions Of The Level Curve



Contours Html



Calculus Iii Exam Iii Notes And Links Math Resources Vosbury V2 0



Level Sets Ximera



0 3 Visualizing Functions Of Several Variables



Level Curves And Contour Plots Mathonline



Problems Elliptic Paraboloid



Solved 3 Bellow Three Contour Maps Are Shown They Chegg Com




Level Surfaces




16 1 Functions Of Several Variables



Chapter 14 Partial Derivatives Ppt Video Online Download



Level Curves And Contour Plots Mathonline



Elliptic Paraboloid The Rejbrand Encyclopaedia Of Curves And Surfaces




Level Curves And Contour Maps Calculus 3 Youtube




Paraboloid Level Curves 8 In Ubqe9xja8 By Bachman
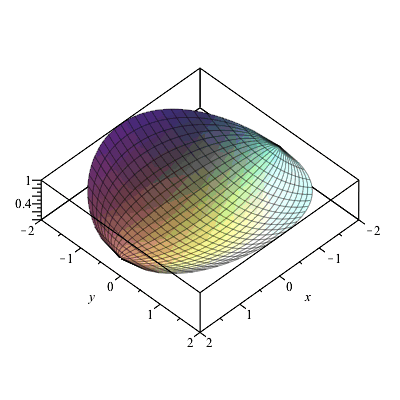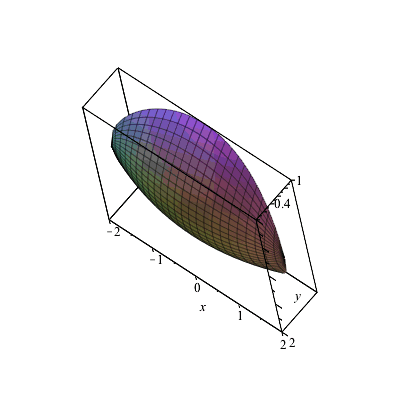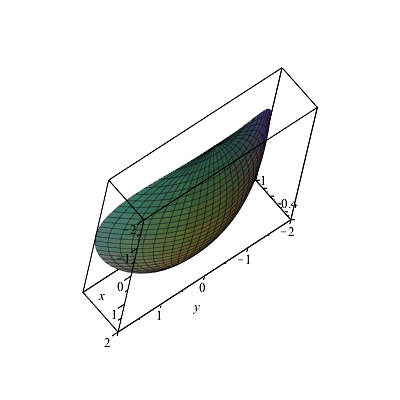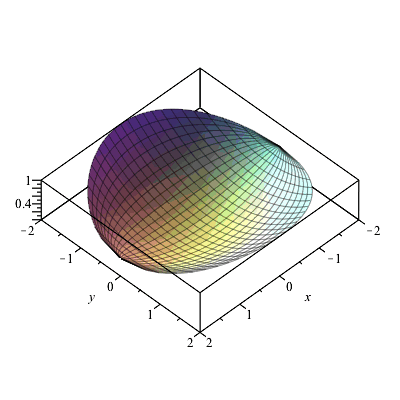



Partial Derivatives Gradients And Plotting Level Curves



Answer In Differential Geometry Topology For Runali 1356



2




Level Curves



Level Curves Part 1b Hyperbolic Paraboloid Youtube
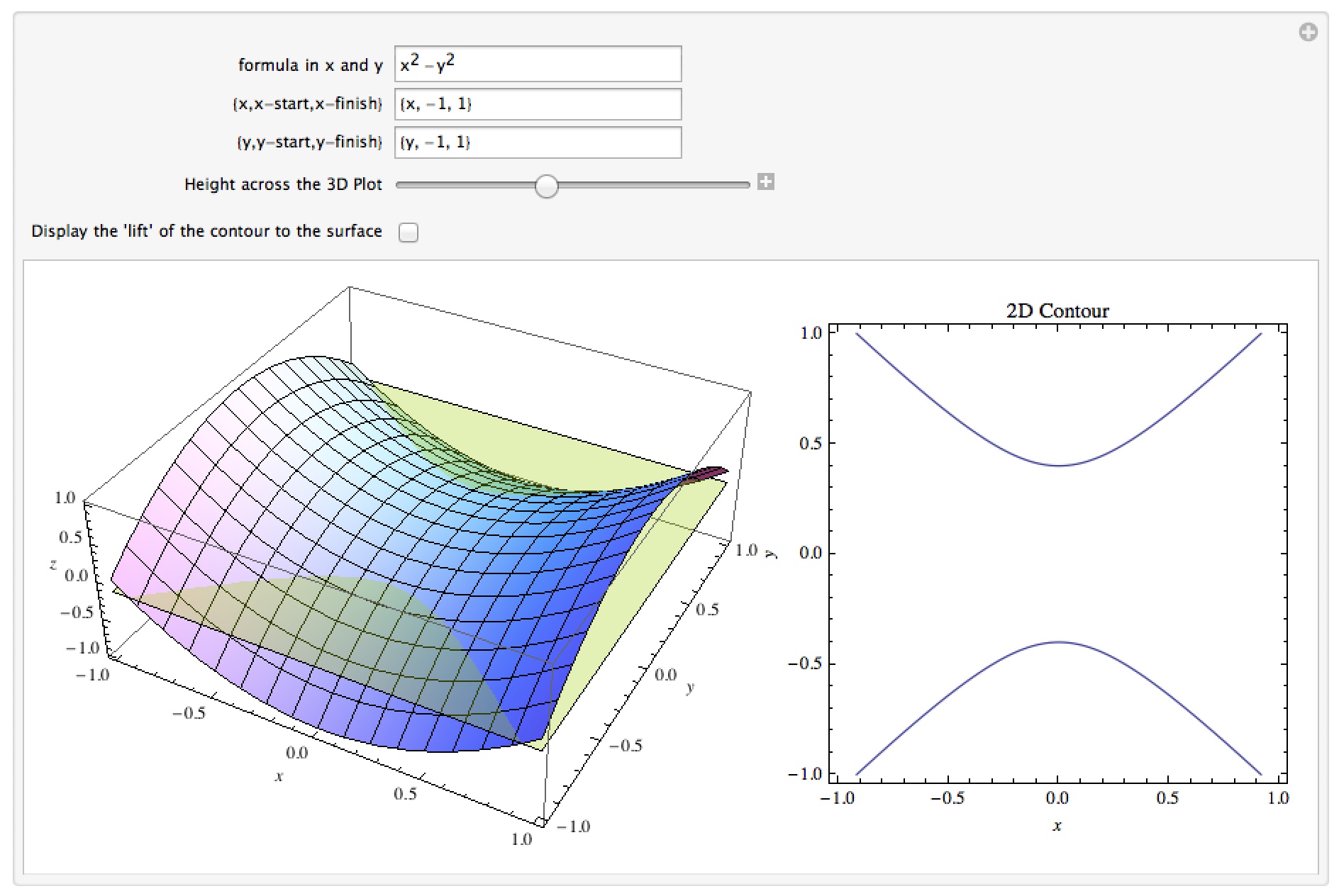



Dr Moretti S Mathematica Notebooks Calculus 3



Answer In Differential Geometry Topology For Shweta 1350




Answered X Y Level Curves Consider The Bartleby



Calc Iv Project 1 Pictures



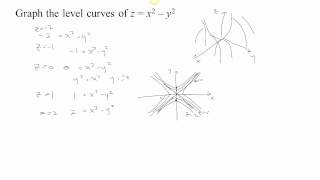
Latex Pictures
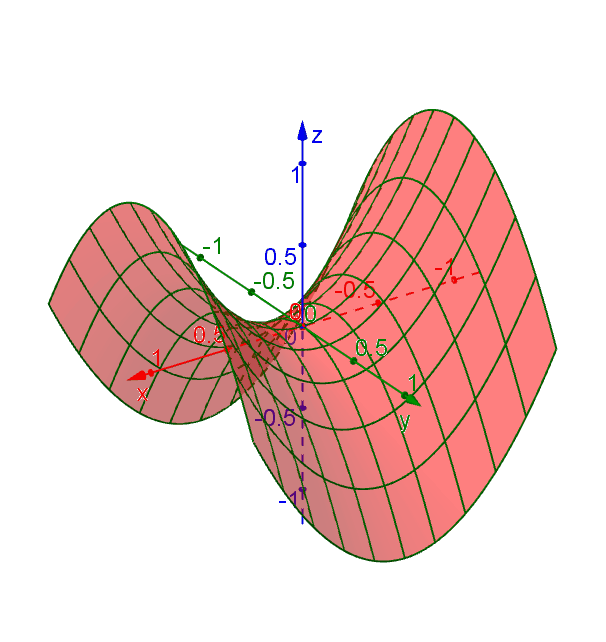



Hyperbolic Paraboloid Geogebra Dynamic Worksheet
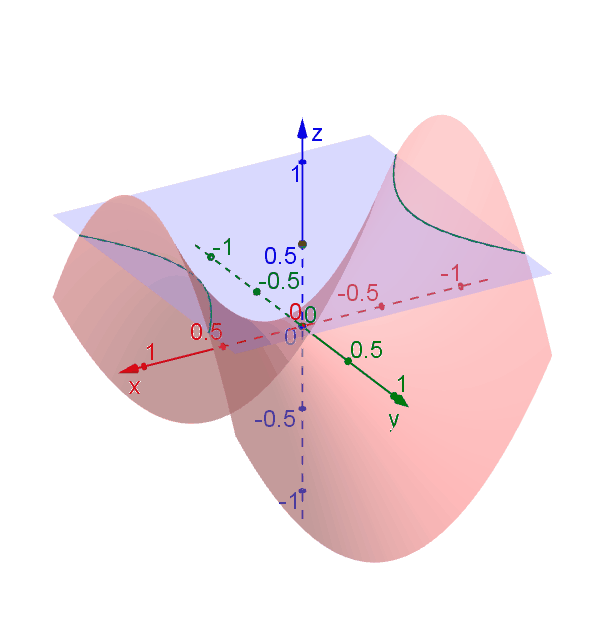



Hyperbolic Paraboloid Geogebra Dynamic Worksheet




Hyperbolic Paraboloid With Level Curves M3dp Net




Answered Question 3 Describe And Sketch The Bartleby
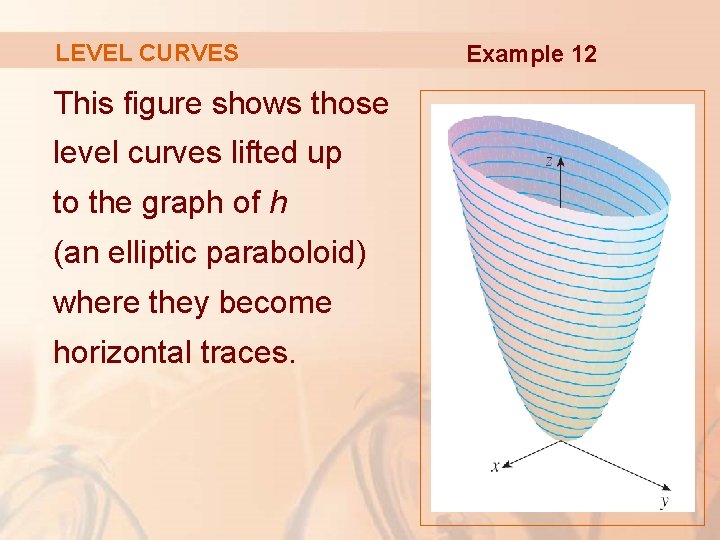



14 Partial Derivatives Partial Derivatives So Far We




What Does It Imply When Two Lines Cross Each Other In A Level Curve Mathematics Stack Exchange




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Level Curves And Contour Plots Mathonline




Why Is The Gradient Related To The Normal Vector To A Surface Continuous Everywhere But Differentiable Nowhere


